En la naturaleza podemos observar patrones que pueden ser estudiados a través de principios matemáticos y que nos permiten apreciar un orden en la vida y la creación, a continuación describimos 2 conceptos matemáticos que podemos encontrar en la naturaleza por todas partes: Los Fractales y la Sucesión de Fibonacci.
FRACTALES

Un fractal es un objeto geométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas. El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal. La propiedad matemática clave de un objeto genuinamente fractal es que su dimensión métrica fractal es un número no entero.
Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el seno de la teoría de la medida.
Fuente: wikipedia/Fractal
Los Fractales guardan autosimilitud (exacta o aproximada), es decir parece que están hechos de copias reducidas de ellos mismos. Se suelen definir por métodos recursivos, operaciones que se repiten una y otra vez, como ocurre con el copo de nieve de Koch:
Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el seno de la teoría de la medida.
Fuente: wikipedia/Fractal
Los Fractales guardan autosimilitud (exacta o aproximada), es decir parece que están hechos de copias reducidas de ellos mismos. Se suelen definir por métodos recursivos, operaciones que se repiten una y otra vez, como ocurre con el copo de nieve de Koch:

Mandelbrot sostenía que los fractales son en realidad mucho más naturales y más comprensibles intuitivamente que los objetos basados en la geometría euclídea, que han sido suavizados artificialmente:
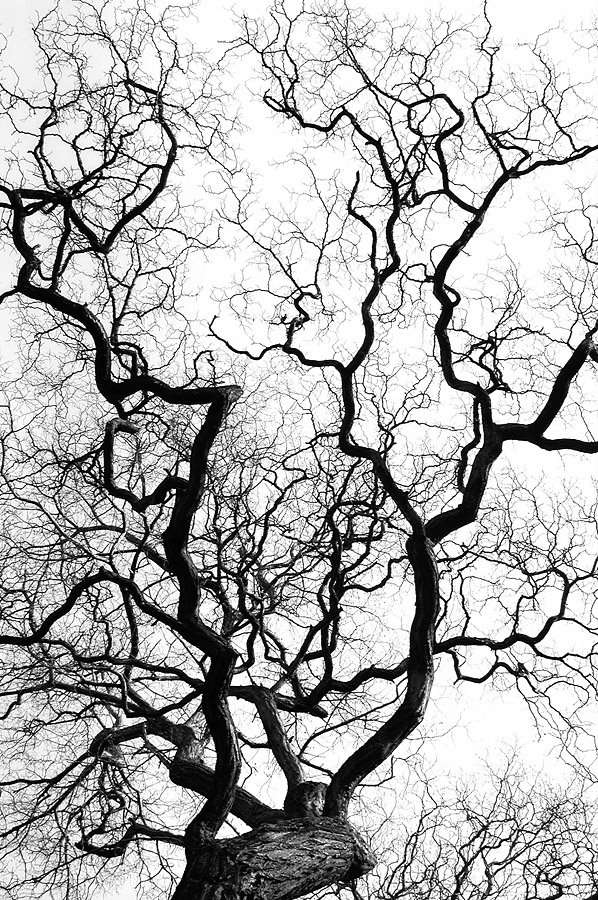
«Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta» Mandelbrot.
«Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta» Mandelbrot.
FOTOS DE ALGUNOS FRACTALES EN LA NATURALEZA









Video: Fractales - A la caza de la dimensión oculta
Última edición por Espiritista el Miér Dic 07, 2016 4:49 pm, editado 2 veces
_________________
Me retracto de toda opinión (incluyendo todos mi artículos y mensajes publicados antes del 23/04/22), y de toda afirmación en cuanto a creencias, costumbres o cualquier afiliación al Espiritismo o a cualquier otra creencia oculta, o a cualquier religión. Me declaro seguidor del camino de Jesucristo. Jesucristo es mi Señor y Salvador. Y creo en la Biblia de inicio a fin, como Palabra de Dios revelada a los hombres. Ya no soy Espiritista, soy Cristiano
Ver explicación en el tema: Ya no soy Espiritista, ver revelaciones en la sala: Desvelando la Realidad y allí encontrarás un Indice de las Revelaciones
Ver explicación en el tema: Ya no soy Espiritista, ver revelaciones en la sala: Desvelando la Realidad y allí encontrarás un Indice de las Revelaciones



